A case-exploration about tangent circles giving some conics

(I worked on this write-up as my 9th finished one on Nov. 2, 2009. Cool!)

Chen Tian

Important Clarification of the following Defintion:

A circle, in Euclidean geometry, is a set of points in a plane which are equidistant from a given point called the center. The common distance of the points of a circle from its center is called its radius.

So when a circle is completely inside another is also called disjoint from it.

Look at the picture above. It is only one case when the two green circles don't meet each other or when they are disjoint.

First, let's play with the script tool for a while to make sure you know how to construct a circle tangent to the other two and pay attention to the locii of the center C of the circle when moving point D along the circumference of circle A and changing the relative positions of circle A and circle B. (To move point D, we can use the function "animation objects" under "display" in the tool bar of Sketchpad. To trace point C, we can use the function "trace" under "display" in the tool bar of Sketchpad.)

Now let's illustrate some cases below. Let R be the radius of circle R, r be the radius of circle B, and x be the radius of circle C. Since there is no difference between the roles of circle A and circle B, we only talk about those cases when either one circle is smaller than the other.

Case 1: Circle B is entirely inside Circle A.

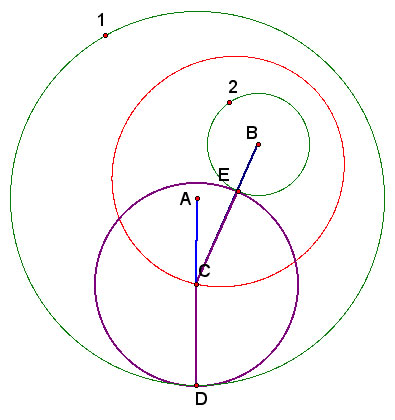
The locus of point C is an ellipse shown in the left-hand-side figure above.

Why? Look at the right-hand-side figure.

|AC|+|BC|=(R-x)+(r+x)=R+r, which is a constant if R and r are given. This is exactly the definition of an ellipse in plane analytic geometry.

Note when circle A and circle B are concentric the locus is simply a circle, of course, shown in the figure below.

Case 2: Circle B intersects with circle A.

The locus of point C is still an ellipse shown in the above figure, for the same reason.

Case 3: Circle B is tangent to circle A.

The locus of point C shrinks to a segment CB shown in the above figure, since R=x, A and C coincide.

Case 4: Circle B is outside of circle A.

What a wonderful trajectory! The locus of point C is a hyperbola shown in the above figure.

Why?

Let's see.

|AC|=|CD|-|AD|=x-R

|BC|=|CE|+|EB|=x+r

So ||AC|-|BC||=|(x-R)-(x-r)|=|R-r|, which is a constant if R and r are given. This is exactly the definition of a hyperbola in plane analytic geometry.

Note in the below case when line j and k are parallel, we will never get the "isosceles triangle" by our construction, and line k will be one of the asymptote of the hyperbola.

Last but not least, why couldn't we get a "parabola"? Recall the definition of a parabola is that the locus of points in a plane which are equidistant to a given point (the focus) and to a given line (the directrix). But there is no fixed line in our construstion.

But we can take one of the two branches of the hyperbola as a "fake parabola" if we take point A as the focus and construct the directrix as shown in the figure below.

All these above, I think, can be used in classrooms for students to explore in order to help them understand better those geometric concepts involved in this assignment.

Return to my homepage for EMAT 6680